Challenge 1: Define the experiment.

First we define how the experiment works. Here, we will simulate a two-armed bandit experiment. In the two-armed bandit task participants repeatedly choose between two stimuli. Each stimulus has a certain reward probability. Participants complete several trials and their goal is to maximize rewards.

Step 1: Define the number of trials and reward probabilities.

First, we have to decide on the number of trials and the reward probabilities for each stimulus. Store the number of trials in a variable T and store the reward probabilities (one for each of the two stimuli) in variable mu.

Note: You can define these parameters however you want. In the Collins paper there were 100 trials and the reward probabilities were .2 for one stimulus and .8 for the other.

Enter your code here:

Check the solution below:

T = 100
mu = [.2, .8]

Step 2: Write the reward function.

The reward function allocates reward stochastically based on reward probabilities. This function uses an action and the reward probabilities as inputs and returns either a reward of 1 or no reward (0).

It achieves this by generating a random number from a uniform distribution ranging from 0 and 1 (in Python you can do this using np.random.random()).

Next, it compares the reward probability associated with the chosen action mu[action] to that number. If it is lower or equal <= to the reward probability it returns 1 (reward) otherwise it returns 0 (no reward).

Note, in python you implement functions by writing:```def allocate_reward(action, mu): # choice and mu are your inputs ... return reward # reward is your return value

You implement if statements, by writing:```if ...:
    ...
else:
    ...

Enter your code here:

Check the solution below:

def allocate_reward(action, mu):
    if np.random.random() < mu[action]:
        return 1
    else:
        return 0

Challenge 2: Set up your first behavioral model (Rescorla-Wagner).

The Rescorla-Wagner model consists of a softmax choice rule and a Q-learning update algorithm. Initially, the model does not know which action is the best choice, so both actions should have the same Q-value.

Step 1: Initialize your Q-values

In this step you define the initial Q-values. Store them in a variable Q.

Note: We will need to run some calculations with these Q-values. To allow for this you’ll have to place your Q-values into a numpy array np.array([...,...]). The initial values should not matter much, but Collins et al. set them to .5.

Enter your code here:

Check the solution below:

Q = np.array([0.5, 0.5])

Step 2: Implement the softmax function.

The softmax function determines choice probabilities based on Q-values using the following formula:

$p_a = \dfrac{exp(Q_{at}*beta)} {\Sigma{exp(Q_{at}*beta)}}$

As you can see, this function also introduces our first participant parameter the inverse temperature (beta). The larger beta the more deterministic (less random) a person's choices are.

Bonus Question:What else does this function do, next to introducing beta?

2.2 Define beta

First define beta and store it in the variable beta. Here you can pick any positive value (we chose 4).

Bonus Question:Why does beta need to be positive?

Enter your code here:

Check the solution below:

beta = 4

2.3 Implement the softmax function.

Note, remember in python you implement functions by writing:def softmax(Q, beta): # Q and beta are your inputs ... return p # p is your return value

To exponentiate an array you use np.exp() and to calculate the sum of an array, you use np.sum().

Enter your code here:

Check the solution below:

def softmax(Q, beta):
    p = np.exp(Q*beta) / sum(np.exp(Q*beta))
    return p

Step 3: Write a decision function.

This function uses choice probabilities as an input and returns a concrete choice as an output. It achieves this by first generating a random number from a uniform distribution ranging from 0 and 1 (in Python you can do this using np.random.random()).

Next, it compares the first choice probability to this number. If it is lower or equal to the choice probability the chosen action is 0, else the chosen action is 1.

Note: Call this function choose(). You will need an if statement. Remember, in Python, you define this as:

if ...: ... else: ...

Enter your code here:

Check the solution below:

def choose(p):
    random_number = np.random.random()
    if random_number <= p[0]:
        return 0
    else:
        return 1

Step 4: Write the update function

The update function updates Q-values based on the reward, according to this formula: $Q_{a,t+1} = Q_{a,t} + \alpha (r - Q_{a,t})$

As you can see, this function introduces another participant parameter: the learning rate (alpha).

4.1 Define alpha

Pick a value between 0 and 1 (we chose .2) and store it as alpha.

Enter your code here:

Check the solution below:

alpha = .2

4.2: Write the update function

Call this function update_q_value() with Q, action, reward, and alpha as inputs and updated_q and delta as outputs. This function first calculates the prediction error and then updates Q.

Enter your code here:

Check the solution below:

def update_q(Q, action, reward, alpha):
    delta = reward - Q[action] # prediction error
    Q[action] = Q[action] + alpha * delta
    return Q, delta

Step 5: Putting it all together

Congratulations, you created all the components of your simulation function. Now let's put them all together and simulate some data. The simulation function (call it simulate_M3RescorlaWagner_v1) takes the experiment parameters, mu and T, as well as the participant parameters alpha and beta as inputs.

Note: Don’t forget to initialize the q-values as we did in step 2.1.

In each trial, we simulate an action chosen by the participant, allocate a reward, and update the participant's q-values accordingly.

Note: In Python you write loops like this:

for t in range(T): ...

As outputs it returns the lists (i.e., vectors) actions, rewards, Qs, and deltas for each trial.

Note: You create vectors like this actions = [] and add data to a vector like this: actions.append(action).

Warning: For technical reasons, when you append Q to Qs, you have to append a copy of Q with Qs.append(Q.copy())

Enter your code here:

Check the solution below:

def simulate_M3RescorlaWagner_v1(T, mu, alpha, beta):
    Qs = []
    deltas = []
    actions = []
    rewards = []
    
    Q = np.array([.5, .5])

    for t in range(T): 
        Qs.append(Q.copy())
        p = softmax(Q, beta)
        action = choose(p)
        reward = allocate_reward(action, mu)
        Q, delta = update_q(Q, action, reward, alpha)
        rewards.append(reward)
        actions.append(action) 
        deltas.append(delta)

    return actions, rewards, Qs, deltas
        

Challenge 3: Explore the parameters

We already wrote you a little function that simply uses your simulate_M3RescorlaWagner_v1 function to simulate an experiment based on your parameters and plots its outputs in a figure. Below, we will go through some parameter combinations and explore their effects.

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

plot_rescorla_game[source]

plot_rescorla_game(T, mu, alpha, beta)

Here are some example parameter values:

T = 100 # number of trials
mu = [.2,.8] # reward probabilities
alpha = .2 # learning rate
beta = 4 # inverse temperature
plot_rescorla_game(T, mu, alpha, beta)

Reducing the learning rate (participant does not manage to learn probabilities)

T = 100 # number of trials
mu = [.2,.8] # reward probabilities
alpha = .01 # learning rate
beta = 4 # inverse temperature
plot_rescorla_game(T, mu, alpha, beta)

Let's give them more trials

T = 1000 # number of trials
mu = [.2,.8] # reward probabilities
alpha = .01 # learning rate
beta = 4 # inverse temperature
plot_rescorla_game(T, mu, alpha, beta)

An extreme beta value makes participants stop exploring.

T = 1000 # number of trials
mu = [.2,.8] # reward probabilities
alpha = .1 # learning rate
beta = 1000 # inverse temperature
plot_rescorla_game(T, mu, alpha, beta)

If beta is very low, participants still learn, but they don't use that knowledge (something that we cannot see in this plot yet).

T = 1000 # number of trials
mu = [.2,.8] # reward probabilities
alpha = .1 # learning rate
beta = .0000000001 # inverse temperature
plot_rescorla_game(T, mu, alpha, beta)

Challenge 4: Choice Kernel

The only difference between choice kernel and rescorla-wagner is that the softmax function takes choice_kernel values instead of Q-values as inputs and the update function is indendent of rewards. Therefore, we only need to change the update function.

Step 1: Write a new update function

The formula of the update function looks like this:

$CK_{a,t+1} = CK_{a,t} + \alpha * 1$

Before the choice kernel is updated, both choice kernels decay with the inverse of the learning rate:

$CK_{t+1} = CK_{t} * (1 - \alpha)$

Call this function update_choice_kernels, with the inputs choice_kernel, action, and alpha.

Note: If you’re confused by the multiplication with one: This is only for comparability with the Rescorla-Wagner.

Enter your code here:

Check the solution below:

def update_choice_kernels(choice_kernel, action, alpha):
    choice_kernel = (1 - alpha) * choice_kernel
    choice_kernel[action] = choice_kernel[action] + alpha * 1
    return choice_kernel

Step 2: Putting it all together.

Now make a simulate_M4ChoiceKernel_v1 function similar to the rescorla wagner function but with our new update function and choice kernels instead of Qs.

Enter your code here:

Check the solution below:

simulate_M4ChoiceKernel_v1[source]

simulate_M4ChoiceKernel_v1(T, mu, alpha, beta)

Note that choice_kernel decays with the inverted alpha in each trial choice_kernel = (1 - alpha_c) * choice_kernel

Challenge 5: Explore the parameters of your choice kernel simulations

plot_choice_kernel_game[source]

plot_choice_kernel_game(T, mu, alpha, beta)

T = 100 # number of trials
mu = [.2,.8] # reward probabilities
alpha = .2 # learning rate
beta = 4 # inverse temperature
actions = plot_choice_kernel_game(T, mu, alpha, beta)

T = 100 # number of trials
mu = [.2,.8] # reward probabilities
alpha = .2 # learning rate
beta = .004 # inverse temperature
actions = plot_choice_kernel_game(T, mu, alpha, beta)

T = 500 # number of trials
mu = [.2,.8] # reward probabilities
alpha = .2 # learning rate
beta = 4 # inverse temperature
actions = plot_choice_kernel_game(T, mu, alpha, beta)

With a reasonably high beta one of the options should always move towards 1.

Reproducing Collins' figures

Challenge 6: Reproducing Panel A

Panel A shows the different in the probability of sticking to the same action (y-axis) depending on whether the last trial was a win or a loss (x-axis), split up by learning model (colors). Here, we will only focus on the Rescorla-Wagner and the Choice Kernel model.

Step 1

Write a fuction that first defines last_action and last_reward. Then determines whether a trial was a stay or switch trial. Finally it calculates the proportion of stay trials depending on whether the last trial was rewarded or not rewarded and outputs the score for each case.

You can use df.action.shift(1) to create variables that represent the value of the last row.

def analysis_WSLS_v1(df):
    # Shifting data back by one
    df['last_action'] = df.action.shift(1)
    df['last_reward'] = df.reward.shift(1)
    # Deciding whether trial is stay trial
    df['stay'] = (df.action == df.last_action).astype(int)
    # Calculating mean stay by case and outputing as series
    output = df.groupby(['last_reward']).stay.mean()
    loseStay = output.loc[0]
    winStay = output.loc[1]
    s = pd.Series([loseStay, winStay])
    return s

Step 2

Simulate data for 110 participants using the Rescorla-Wagner model and store their proportion of stay trials depending on the last trial's reward in a dataframe. Finally, you calculate the mean proportion of stay trials (for wins and losses) over all participants (call the variable rw), which we will use in the plot.

For this, we will use the same experiment and participant parameters as Collins, below:

T = 100 
mu = [.2,.8]
alpha = .1
beta = 5
participants = 110

Note: To turn the actions and rewards into a dataframe, you can use df = pd.DataFrame({’action’:actions, ’reward’:rewards}).

Enter your code here:

Check the solution below:

data = []
for i in range(participants):
    actions, rewards, Cks, _ = simulate_M3RescorlaWagner_v1(T, mu, alpha, beta)
    df = pd.DataFrame({'action':actions, 'reward':rewards})
    data.append(analysis_WSLS_v1(df))
df = pd.DataFrame(data)
df.columns = ['loseStay','winStay']
rw = df.mean()

rw.plot()
sns.despine()

To see if this worked, let's plot the result.

Step 3

Now do the same for the choice kernel and call the variable ck. Note that for this, Collins changed beta to 3.

Enter your code here:

Check the solution below:

beta = 3 # inverse temperature
data = []
for i in range(participants):
    actions, rewards, Cks = simulate_M4ChoiceKernel_v1(T, mu, alpha, beta)
    df = pd.DataFrame({'action':actions, 'reward':rewards})
    data.append(analysis_WSLS_v1(df))
df = pd.DataFrame(data)
df.columns = ['loseStay','winStay']
ck = df.mean()

Step 4

We plot everything together.

ax = rw.plot()
ax = ck.plot(ax = ax)
sns.despine()

Challenge 7: Reproducing Panel B

To create Panel B, we simulate the proportion of correct choices (y-axis) split by different values of alpha (x-axis) and beta (colors), split by early (first ten) and late (last ten) trials (subpanels). These are the alphas and betas that Collins uses for this plot:

alphas = list(np.arange(.02, 1.02, .02))
betas = [1,2,5,10,20]

Step 1

Write a nested loop that loops through 200 simulations, all alphas, and all betas. In each iteration it simulates data using the Rescorla-Wagner model and outputs the proportion of correct choices (a choice is correct when the stimulus that is more likely to return a reward is picked) in the first and last ten trials.

Note: To store the output first make a data list and in each iteration make a session dictionary which you append to the data list.

Note: To get the correct action (i.e. the action associated with the highest reward probability, us np.argmax(mu).

Note: Collins runs 1000 simulations, but because our code runs a bit slow, we recommend doing this 200 per alpha beta combination.

Enter your code here:

Check the solution below:

%%time
data = []
for i in range(200):
    for alpha in alphas:
        for beta in betas:
            a, r, _, _ = simulate_M3RescorlaWagner_v1(T, mu, alpha, beta)
            session_dict = {}
            session_dict['alpha'] = alpha
            session_dict['beta'] = beta
            
            imax = np.argmax(mu) # Mu max index
            a = pd.Series(a)
            session_dict['correct_early'] = (a.iloc[:10] == imax).mean()
            session_dict['correct_late'] = (a.iloc[-10:] == imax).mean()
            data.append(session_dict)
            
df = pd.DataFrame(data) 

Step 2

Let's plot this all together.

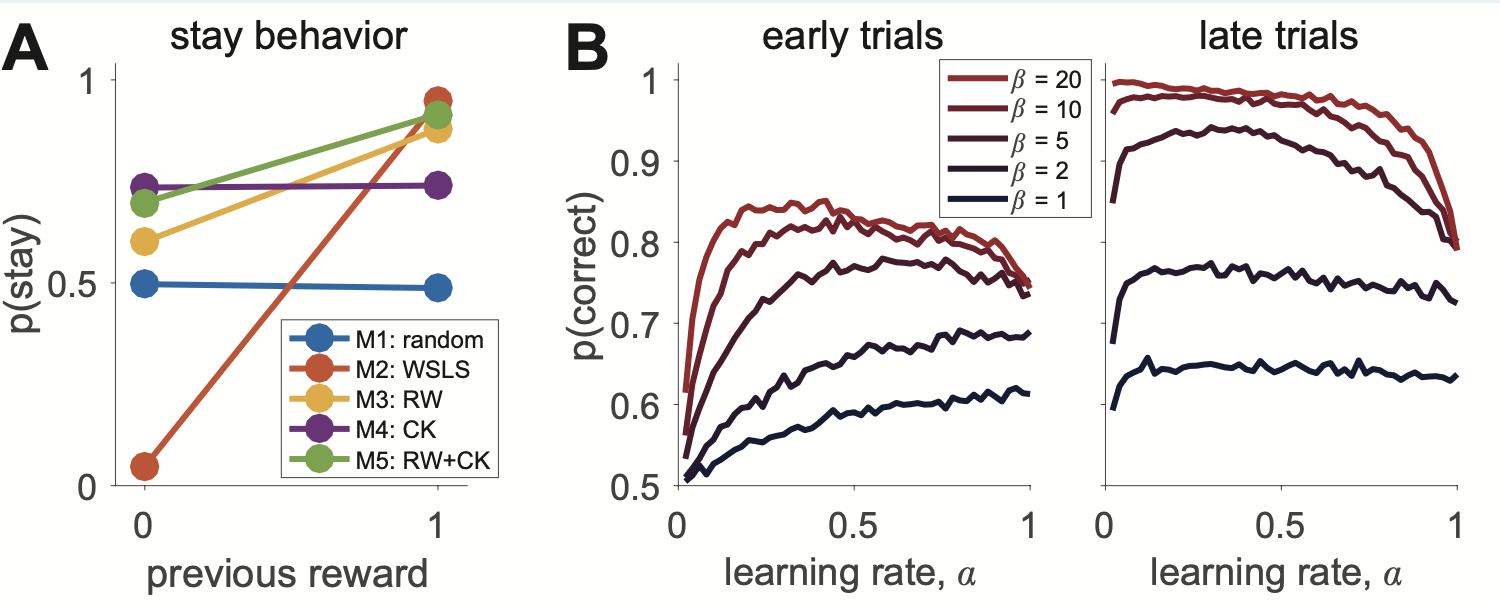
Note: You can use fig, axs = plt.subplots(1,2, figsize = (14,7)) to make a figure with several plots in it; you can use sns.lineplot to make nice lineplots; this also lets you chose the color palette (we already chose sns.color_palette("rocket_r")[:5]).

Enter your code here:

Check the solution below:

palette = sns.color_palette("rocket_r")[:5]
fig, axs = plt.subplots(1,2, figsize = (14,7))

sns.lineplot(x = 'alpha', y = 'correct_early', hue = 'beta', ci = None, data = df, ax = axs[0], legend = True, palette = palette)
#

sns.lineplot(x = 'alpha', y = 'correct_late', hue = 'beta', ci = None, data = df, ax = axs[1], palette = palette, legend = False)
axs[0].legend(loc='upper right', bbox_to_anchor=(1.1, 1))
axs[0].set_title("early trials")
axs[1].set_title("late trials")

sns.despine()

Well done! :)

Bonus Challenge: Combine all plots to make them look exactly as Collins'.

Enter your code here:

Check the solution below: